Micad'Eau
Projet financé par la DGCIS, la région Ile De France et le Conseil Général des Yvelines
Partenaires : Advitam, Suez Environnement, EFS, IFSTTAR, ESIEE
Dans le cadre du projet Micad'eau, on s'intéresse à la détection d'anomalies (fuite, apparition de polluants) dans des réseaux d'eau potable. Et plus particulièrement à la reconstruction de l'écoulement dans les canalisations grâce à des modèles inverses et des mesures ponctuelles faites par des capteurs. Cependant, malgré des moyens de calculs toujours plus performants, la résolution du problème inverse va être limitée par des problèmes de taille mémoire et des temps de calculs trop longs. Ceci interdit toute identification en temps "réel" ou "pseudo-réel", comme on le souhaiterait.
Afin de pallier ces difficultés, une voie consiste à utiliser des modèles simplifiés qui vont permettre d'obtenir des résultats approchés satisfaisants en des temps acceptables.
Méthode de réduction
Toutefois, il ne faut pas oublier que les équations qu'on souhaite résoudre dépendent de paramètres servant à identifier des configurations particulières (la géométrie, des propriétés physiques, ...). Les méthodes de réductions telles que la POD, CRB (certified reduced basis) nécessitent souvent d'avoir un accès direct au code de simulation. Grâce à une méthode non intrusive de base réduite il serait tout de même possible de faire de la réduction de modèle en utilisant un logiciel en boîte noire.
Cette méthode repose sur le fait que, les coefficients de la solution dans la base réduite, peuvent être calculés comme l'intégrale de cette solution avec les éléments de base réduite orthonormés. La précision de ces moments ne nécessite pas la convergence dans les normes de l'énergie mais dans des normes plus faibles (négatives). Leur approximation peut donc être optimale, tout en diminuant le nombre de degrés de liberté, et ce, même dans le cas d'un code utilisable uniquement en boîte noire. Il n'est pas nécessaire de modifier ou même d'avoir accès au code source pour implémenter cette méthode, toutes les étapes étant effectuées en externe.
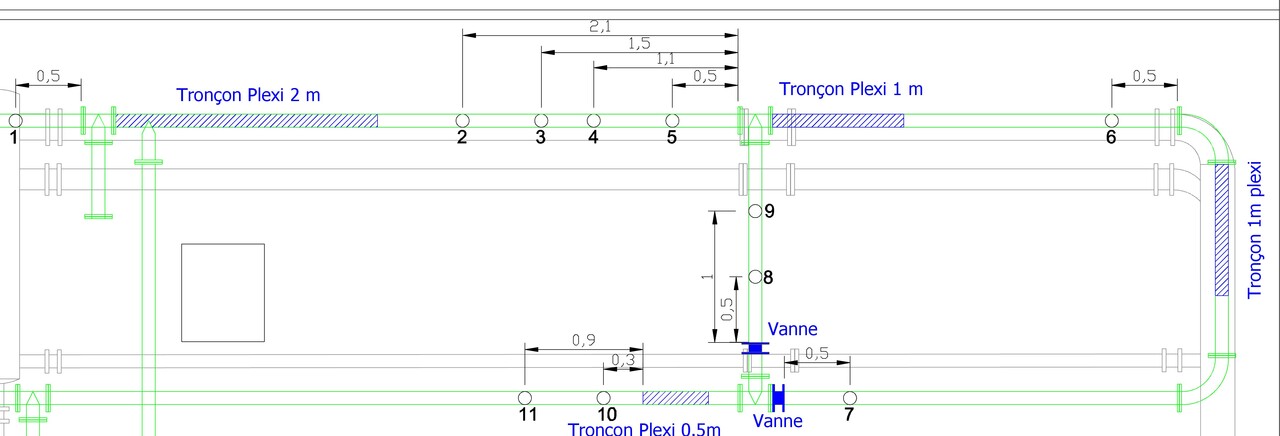
Dans l'exemple suivant on souhaite faire varier l'amplitude de la vitesse à l'entrée dans une canalisation, entre 0.01 et 0.5 cm/s
On a utilisé le logiciel "Freefem++" comme pseudo boîte noire, pour la résolution du problème Navier-Stokes stationnaire. Celui-ci a été implanté à l'aide de la méthode des éléments finis combinée à une méthode de Newton (pour prendre en compte les termes non linéaires).
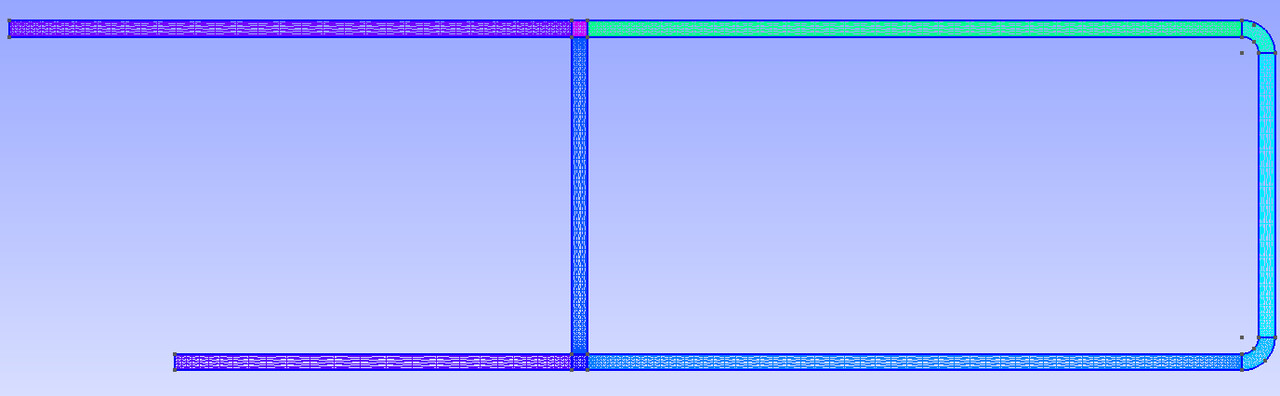
Pour valider la méthode de bases réduites non intrusive, on dispose de solutions calculées sur un maillage fin et sur un maillage grossier.
Maillage fin
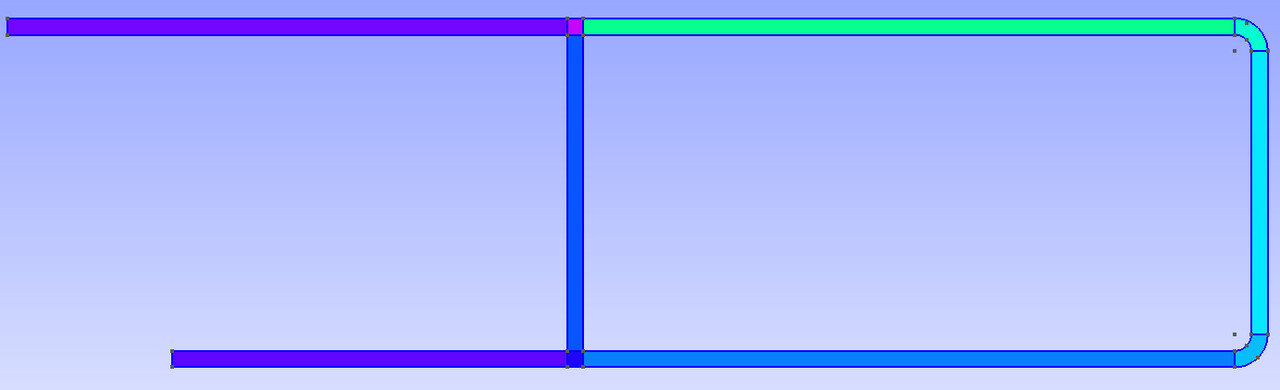
Maillage grossier
Méthodes inverses
L'objectif est de réaliser une cartographie de l'écoulement et du champ de concentration en chlore dans un réseau d'eau potable. Pour cela, nous avons développé des méthodes inverses exploitant des mesures in-situ et des modèles mathématiques : équations de la mécanique des fluides et équations de transport-diffusion-réaction. Ces méthodes s'appuient sur la théorie du contrôle optimal : on cherche les paramètres de contrôle, e.g. conditions limites en vitesse, permettant de minimiser une fonctionnelle d'écart entre simulation numérique et mesure. Ce problème de minimisation est résolu à l'aide d'une méthode de type gradient où le gradient de la fonctionnelle est calculé à moindre coût grâce à l'état adjoint. Dans la suite, nous présentons un aperçu des travaux réalisés.
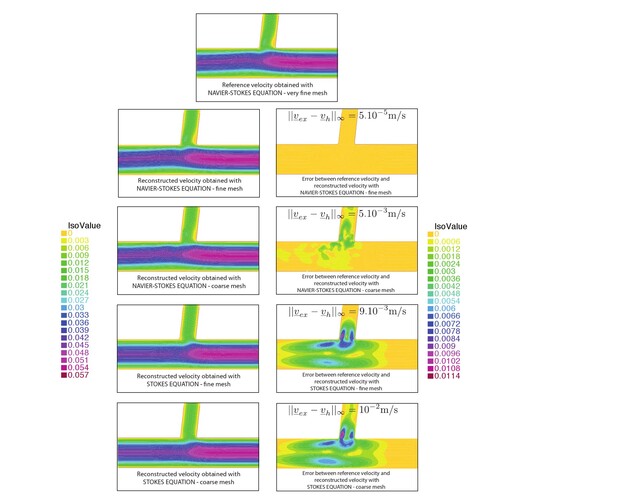
Reconstruction d'un écoulement instationnaire par modélisation inverse
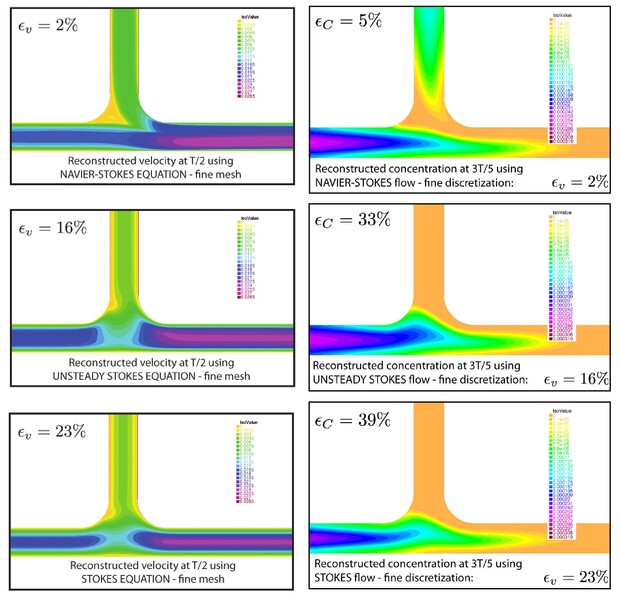
Sur le cas-test d'une jonction en forme de Té, nous avons utilisé différents modèles physiques (équations de Stokes, équations de Navier-Stokes) dans le processus de reconstruction. Nous avons montré que l'utilisation d'un modèle simplifié d'écoulement (équation de Stokes) afin de reconstruire un écoulement de type Navier-Stokes pouvait entraîner une erreur de 20% sur le champ de vitesse. Afin d'obtenir une erreur de l'ordre de 1% sur le champ de vitesse reconstruit dans un réseau d'eau potable, une méthode hybride a été proposée. Cette méthode consiste à reconstruire l'écoulement dans l'ensemble du réseau par modélisation inverse avec un modèle simplifié (équation de Stokes) et ensuite à réaliser une résolution directe Navier-Stokes dans les jonctions.
Reconstruction de la concentration en chlore par modélisation inverse
Une méthode inverse a été proposée afin de reconstruire en 2D le champ de concentration en chlore. L’écoulement était supposé connu. Sur le cas-test d’une jonction en forme de Té, nous avons étudié l’influence de plusieurs paramètres sur la qualité du champ reconstruit de concentration en chlore : e.g. l’influence de l’erreur de discrétisation des équations de transport-diffusion-réaction, l’influence des incertitudes sur l’écoulement, l’influence des erreurs de mesure. On note qu’une erreur de 20% sur l’écoulement peut entraîner une erreur de reconstruction de 40% sur le champ de concentration en chlore.
Positionnement optimal des capteurs de chlore : application sur une canalisation en forme de Té
Afin de déterminer l’emplacement optimal des capteurs de chlore au vu de la reconstruction du champ de chlore, un outil numérique peu coûteux en temps de calcul été développé. Celui-ci est fondé sur la résolution d’un problème adjoint. La méthode a été illustrée sur une canalisation en forme de Té. Ces travaux ont fait l’objet d’une publication dans la revue internationale “Computers and Mathematics with Applications”.
Identification de la constante de cinétique de réaction dans un réseau d’eau potable
Dans un réseau d’eau potable, le chlore réagit avec de nombreux éléments (organiques, i.e algues, et chimiques) afin d’assurer la qualité de l’eau. Le paramètre de cinétique de réaction du chlore est un des paramètres méconnus dans le réseau d’eau potable. Ainsi, lors du post-doctorat de M. Chabchoub, une méthode inverse a été mise en oeuvre afin de déterminer cette constante de cinétique à partir de mesures et de modèle physique, i.e équations de transport-diffusion-réaction. Grâce au recalage de ce paramètre, nous pouvons obtenir des solutions numériques associées au champ de concentration en chlore plus représentatives de la réalité.
Pour la résolution de ce problème inverse, nous avons utilisé les outils standards de l’Ingénieur en hydraulique : logiciel 0D-1D Epanet avec des développements en C++.
Positionnement optimal des capteurs de chlore
Durant le post-doctorat de M. Mahfoudhi, nous avons adapté et appliqué la méthode de positionnement optimal précédemment proposée à l’ensemble d’un réseau. Pour chaque position de capteurs envisagée, l’objectif était d’apporter des informations quant à l’observabilité de ce capteur. Ainsi, pour une position de capteur donnée, nous étions capable de localiser et quantifier les zones du réseau “noncouvertes” par le capteur, c’est à dire les zones géographiques où on ne pouvait pas identifier le paramètre

JulienWaeytens
Directeur de Recherche
julien.waeytens@univ-eiffel.fr
+33 (0)1 81 66 84 53Marne-la-Vallée
RachidaChakir
Chercheur en Mathématiques Appliquées
+33 (0)1 81 66 84 36Marne-la-Vallée
PatriceChatellier
Chercheur
patrice.chatellier@univ-eiffel.fr
Marne-la-ValléeFrédéricBourquin
Marne-la-Vallée