Au cours de ce projet nous avons développé une démarche de reconstruction de l'écoulement fondée sur la théorie du contrôle optimal. L'objectif était de déterminer les conditions limites de contrôle en vitesse (supposée parabolique sur la section) minimisant l'écart entre la simulation numérique et les mesures. Les grandes étapes de la démarche étaient les suivantes :

• Résolution du problème direct

• Résolution d'un problème adjoint

• Calcul du gradient de la fonctionnelle à l'aide de l'état adjoint

• Résolution du problème de minimisation à l'aide d'une méthode de descente

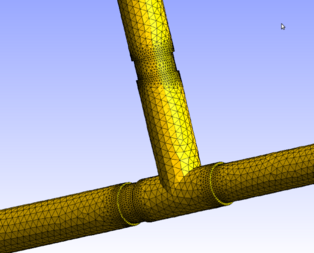
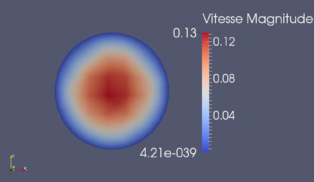
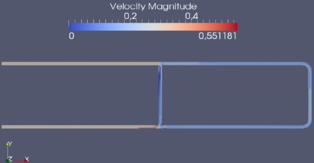
Sur le cas-test 2D d'une ''canalisation en forme de Té", nous avons validé cette méthode pour un grand nombre de modèles d'écoulement : Stokes stationnaire, Stokes instationnaire et Navier-Stokes. De plus, l'influence de l'erreur de discrétisation et de l'erreur de modèle a été étudiée. Ceci a fait l'objet d'une publication.

La méthode précédente permet de reconstruire de manière pertinente l'écoulement. Néanmoins, elle n'est pas adaptée à une reconstruction en temps-réel. De ce fait, nous nous sommes intéressés à une autre approche fondée sur le principe de superposition. L'idée était de réaliser un maximum de calculs ''hors ligne" et un minimum de calculs en temps réel. Cette approche a été validée sur le cas-test de la canalisation en Té et sur deux portion du réseau de villes situées en France. Dans cette partie, nous nous sommes limités à des modèles d'écoulement linéaires (Stokes stationnaire et Stokes instationnaire).

De manière analogue, nous avons étudié la méthode de reconstruction pour le champ de concentration en chlore dans un écoulement connu. Dans ce cas, l'objectif était de déterminer les conditions limites de concentration en chlore (supposée constante sur la section) minimisant l'écart entre la simulation numérique et les mesures. La méthode a été appliquée sur le cas-test de la canalisation en Té. Nous avons montré que le positionnement des capteurs de chlore avait une importance fondamentale.